Question

Graph the system of linear inequalities and shade in the solution set. If there are no solutions, graph the corresponding lines and do not shade in any region X - y > 2 Y < - 1/3x + 1

Answer 1

We need to graph the following inequality system:

`\begin{cases}x-y>2 \\ y<-(1)/(3)x+1\end{cases}`

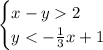
Now we need to isolate the y-variable on the left side for the first equation:

We need to points to graph these equations. We will use the points that have x equal to 0 and y = 0.

For the first equation:

`\begin{gathered} y=0-2 \\ y=-2 \end{gathered}`

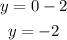
The first point is (0,-2).

`\begin{gathered} 0=x-2 \\ x=2 \end{gathered}`

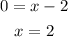
The second point is (2, 0).

For the second equation:

`\begin{gathered} y=-(1)/(3)\cdot0+1 \\ y=1 \end{gathered}`

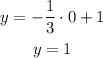
The first point (0,1).

`\begin{gathered} 0=-(1)/(3)x+1 \\ (1)/(3)x+1 \\ x=3 \end{gathered}`

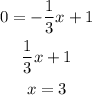
The second point is (3, 0).

Now we can trace both boundary lines:

Finally we can shade the solution set, which is the region that is below both lines, since both have an "<" signal.