Question

2.2.18Find the vertex of the graph of the quadratic function. Determine whether thegraph opens upward or downward, find the y-intercept, and sketch the graph.f(x) = - x2 - 2x+3The vertex is(Simplify your answer. Type an ordered pair.)

Answer 1

The quadratic function is given by the following expression:

`f(x)=-x^2-2x+3`

The direction at which the graph opens is determined by the signal of the number multiplying x². If the number is positive then the graph opens upwards, if it is negative it opens downward. In this case it is negative so it opens donward.

The vertex of a quadratic expression can be found by the following expression:

`x=(-b)/(2a)`

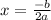
Where a is the number multiplying "x²", while b is the number multiplying "x". Applying the data from the problem we have:

`x=(-(-2))/(2\cdot(-1))=(2)/(-2)=-1`

To find the value of "y" for the vertex we need to apply the coordinate for x on the expression. We have:

`\begin{gathered} f(-1)=-(-1)^2-2\cdot(-1)+3 \\ f(-1)=-1+2+3=4 \end{gathered}`

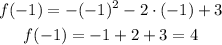
The coordinates of the vertex are (-1,4).

To sketch a graph we need to find the x-intercept and y-intercept of the function. These are given when f(x) = 0 and x=0 respectively. Let's find these points.

`\begin{gathered} 0=-x^2-2x+3 \\ -x^2-2x+3=0 \\ x_(1,2)=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(-1)(3)}}{2\cdot1} \\ x_1=-3 \\ x_2=1 \end{gathered}`
`f(x)=-0^2-2\cdot0+3=3`

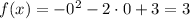
The x intercept happens in two points -3 and 1, while the y intercept happens in the point 3. With this and the vertex we can sketch the function.