Question

Use an explicit formula to find the 10th term of the geometric sequence. 2,8, 32, 128, ...

Answer 1

To find the explicit formula of a geometric sequence you use the next:

`a_n=a_1\cdot r^(n-1)`

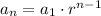
a1 is the first term in the sequence

r is the ratio between each pair of terms

2,8,32,128,...

Find r:

`\begin{gathered} (8)/(2)=4 \\ \\ (32)/(8)=4 \\ \\ (128)/(32)=4 \end{gathered}`

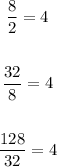
Find the explicit formula:

`a_n=2\cdot4^(n-1)`

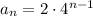
To find the 10th term you substitute the n in the formula for 10:

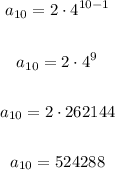
`\begin{gathered} a_(10)=2\cdot4^(10-1) \\ \\ a_(10)=2\cdot4^9_{}_{} \\ \\ a_(10)=2\cdot262144 \\ \\ a_(10)=524288 \end{gathered}`Then, the 10th term is 524,288