In this problem, we have an arithmetic sequence with:
• first term a_1 = -22,
,
• common difference r = 5.
The terms of the arithmetic sequence are given by the following relation:
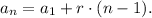
Replacing the values a_1 = -22 and r = 5, we have:
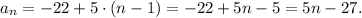
We must compute the sum of the first 30 terms of the sequence.
The sum of the first N terms of a sequence is:
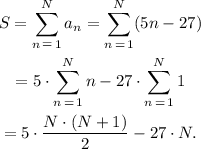
Where we have used the relations:
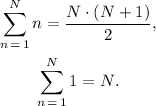
Replacing the value N = 30 in the formula for the sum S, we get:
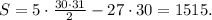
Answer
sum = 1515