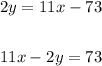Question

Write and equation of a line that passes through the point (5, -9) and is perpendicular to the line 2x + 11y = 22

Answer 1

The general equation of the line in slope - intercept form is :

`y=m\cdot x+b`

Where m is the slope and b is y - intercept

Given the line : 2x + 11y = 22​

We need to write it in slope - intercept form to find the slope of it

so,

`\begin{gathered} 2x+11y=22​ \\ 11y=-2x+22 \\ y=-(2)/(11)x+2 \end{gathered}`

So, the slope of the given line = -2/11

The required line is perpendicular to the given line

So, the product of the slope of the two lines = -1

So, if the slope of the given line is m , the slope of the required line will be = -1/m

So, the slope of the required line = 11/2

The equation of the required line will be :

`y=(11)/(2)x+b`

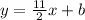
Using the given point ( 5 , -9 ) to find the value of b

So, when x = 5 , y = -9

`\begin{gathered} -9=(11)/(2)\cdot5+b \\ -9=(55)/(2)+b \\ b=-9-(55)/(2)=-(73)/(2) \end{gathered}`

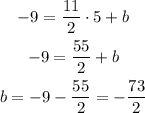
so, the equation of the line is :

`y=(11)/(2)x-(73)/(2)`

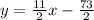
And the standard form will be :

`\begin{gathered} 2y=11x-73 \\ \\ 11x-2y=73 \end{gathered}`