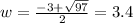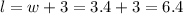Question

Help meeeeeeeeeeeeeeeeeeeeee

Answer 1

To the nearest tenth, the length is 6.4 meters, and the width is 3.4 meters.

Explanation:

Let w be the width of the rectangle. Then l = w + 3, and we have:

`w(w + 3) = 22`

`{w}^(2) + 3w = 22`

`{w}^(2) + 3w - 22 = 0`

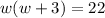
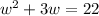
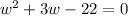
Calculating the discriminant:

`\sqrt{ {3}^(2) - 4(1)( - 22)} = √(9 + 88) = √(97)`

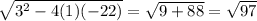
So by the quadratic formula, and discarding the negative solution, we then obtain:

`w = ( - 3 + √(97) )/(2) = 3.4`

`l = w + 3 = 3.4 + 3 = 6.4`