Question

Instructions: For the following real-world problem, solve using any method. Use what you've learned to determine which method would be best. Put your answer in the context of the problem and determine the appropriate final answer. A sprinkler is set to water the backyard flower bed. The stream of water and where it hits the ground at the end of the stream can be modeled by the quadratic equation -22 + 14x + 61 = 0 where x is the distance in feet from the sprinkler. What are the two solutions in exact form? 2 x V X or What are the rounded values (to two decimal places)? Which of these answers makes sense in context to be the value of the number of products? x =

Answer 1

Given the next quadratic equation:

`-x^2+14x+61=0`

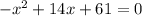
we can use the quadratic formula to solve it, as follows:

`\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{-14\pm\sqrt[]{14^2-4\cdot(-1)\cdot61}}{2\cdot(-1)} \\ x_(1,2)=\frac{-14\pm\sqrt[]{196+244}}{-2} \\ x_(1,2)=\frac{-14\pm\sqrt[]{440}}{-2} \\ x_1=\frac{-14+\sqrt[]{440}}{-2}=(-14)/(-2)-\frac{\sqrt[]{440}}{2}=7-\sqrt[]{110} \\ x_2=\frac{-14-\sqrt[]{440}}{-2}=(-14)/(-2)+\frac{\sqrt[]{440}}{2}=7+\sqrt[]{110} \end{gathered}`

The rounded values (two decimal places) are:

`\begin{gathered} x_1=7-10.49=-3.49 \\ x_2=7+10.49=17.49 \end{gathered}`

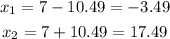
Since x is the distance, in ft, from the sprinkler, it cannot be negative, then the answer which makes sense in the context of this problem is 17.49 ft