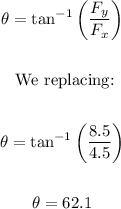Question

A force F1 of magnitude 5.70 units acts on an object at the origin in a direction = 38.0° above the positive x-axis. (See the figure below.) A second force F2 of magnitude 5.00 units acts on the object in the direction of the positive y-axis. Find graphically the magnitude and direction of the resultant force F1 + F2.magnitude unitsdirection ° counterclockwise from the +x-axisTwo forces act on an object. Force vector F1 acts up and right on the right side of the object at an angle above the horizontal. Force vector F2 acts vertically upwards on the top side of the object.

Answer 1

Magnitude: 9.62 units

Direction: 62.1°

Explanation:

Given:

F1 = 5.7 units

F2 = 5 units

Angle () = 38°

The vertical component of force F1 is:

`\begin{gathered} F_(1y)=F_1\cdot\sin\theta \\ \\ \text{ We replacing:} \\ \\ F_(1y)=5.7\cdot\sin(38)=3.5j\text{ units} \end{gathered}`

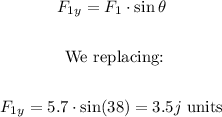
The horizontal component of force F1 is:

`\begin{gathered} F_(1x)=F_1\cdot\cos\theta \\ \\ \text{ We replacing:} \\ \\ F_(1x)=5.7\cdot\cos(38)=4.5i\text{ units} \end{gathered}`

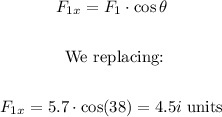
Therefore, the total force F1 is:

`\begin{gathered} F_1=F_(1x)+F_(1y) \\ \\ F_1=4.5i+3.5j \end{gathered}`

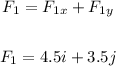
The vertical component of force F2 is:

`F_(2y)=5j\text{ units}`

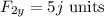
The horizontal component of force F2 is:

`F_(2x)=0i`

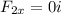
Therefore, the total force F2 is:

`\begin{gathered} F_2=F_(2x)+F_(2y) \\ \\ F_2=0i+5j \end{gathered}`

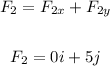
The resultant force (F1 + F2) would be:

`\begin{gathered} F=F_1+F_2 \\ \\ F_=4.5i+3.5j+0i+5j \\ \\ F=4.5i+8.5j \end{gathered}`

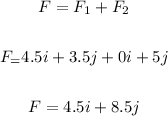
The magnitude of the resultant force is:

`\begin{gathered} F=√((F_x)^2+(F_y)^2) \\ \\ \text{ We replacing:} \\ \\ F=√(4.5^2+8.5^2) \\ \\ F=√(20.25+72.25)=√(92.5) \\ \\ F=9.62\text{ units} \end{gathered}`

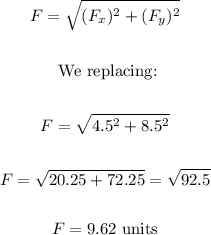
The direction is:

`\begin{gathered} \theta =\tan ^(-1)\left((F_y)/(F_x)\right) \\ \\ \text{ We replacing:} \\ \\ \theta =\tan ^(-1)\left((8.5)/(4.5)\right) \\ \\ \theta=62.1\degree \end{gathered}`