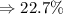Answer:
The number of years for the repayment is
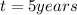
The amount to be repaid back monthly is
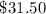
The cost of the laptop given is
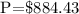
Step 1:
Calculate the total amount of money to be repaid after 5 years

Step 2:
Calculate the interest on the laptop
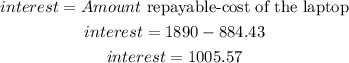
Step 3:
To calculate the interest rate, we will use the formula below
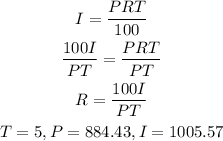
By substituting the values, we will have
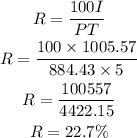
Hence,
The interest rate will be