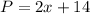Question

Find the area and perimeter of the rectangle based on information given Length = 5 Width = x + 2

Answer 1

Given the length and the expression that represents the width of a rectangle, you need to remember that:

• The area of a rectangle can be calculated by multiplying its dimensions:

`A=lw`

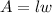
Where "l" is the length and "w" is the width.

• The perimeter of a rectangle is:

`P=2l+2w`

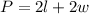
Where "l" is the length and "w" is the width.

Then, knowing that:

`\begin{gathered} l=5 \\ w=x+2 \end{gathered}`

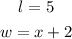
- You can set up that the area of this rectangle is:

`A=5(x+2)`

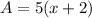
Simplifying, you get:

`\begin{gathered} A=(5)(x)+(5)(2) \\ A=5x+10 \end{gathered}`

- And the perimeter is:

`\begin{gathered} P=(2)(5)+(2)(x+2) \\ P=10+2x+4 \\ P=2x+14 \end{gathered}`

Hence, the answer is:

- The area is:

`A=5x+10`

- The perimeter is:

`P=2x+14`