Question

What is the annual percentage yield (APY) for money invested at an annual rate of(A) 4.09% compounded monthly?(B) 4.1% compounded quarterly?

Answer 1

The annual percentage yield is given by the following formula:

`\text{APY}=(1+(r)/(n))^n-1`

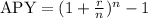
Where r is the stated annual interest rate (in decimal form) and n is the number of times compounded.

A) APY for money invested at an annual rate of 4.09% compounded monthly.

Thus, the annual interest rate in decimal form is:

`r=(4.09\%)/(100\%)=0.0409`

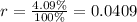
And as it is compounded monthly then n=12.

Replace these values and solve:

`\begin{gathered} \text{APY}=(1+(0.0409)/(12))^(12)-1 \\ \text{APY}=(1+0.0034)^(12)-1 \\ \text{APY}=(1.0034)^(12)-1 \\ \text{APY}=1.0417-1 \\ \text{APY}=0.0417 \end{gathered}`

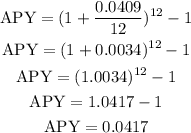
The APY is 0.0417=4.17%.

B) 4.1% compounded quarterly:

The annual interest rate is:

`r=(4.1\%)/(100\%)=0.041`

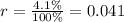
As it is compounded quarterly then n=4.

Replace and solve:

`\begin{gathered} \text{APY}=(1+(0.041)/(4))^4-1 \\ \text{APY}=(1+0.0103)^(12)-1 \\ \text{APY}=(1.0103)^(12)-1 \\ \text{APY}=1.1302-1 \\ \text{APY}=0.1302 \end{gathered}`

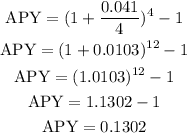
The APY is 0.1302=13.02%