The given formula for Marc's shot is:

a. To prove that the shot actually hung in the air for 15 seconds, we need to replace x=15 in the formula and solve for h, as follows:
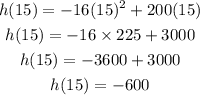
As the height is negative, it means after 15 seconds the ball already hit the ground, because the ground is located at h=0. Then this result proves that this is just another one of Marc's lies.
b. To find how long the ball actually hung in the air, we need to find the x-values that makes h=0, as follows:
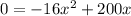
We have a polynomial in the form: ax^2+bx+c=0, where a=-16, b=200 and c=0.
We can use the quadratic formula to solve for x:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-200\pm\sqrt[]{(200)^2-4(-16)(0)}}{2(-16)} \\ x=\frac{-200\pm\sqrt[]{40000+0}}{-32} \\ x=\frac{-200\pm\sqrt[]{40000}}{-32} \\ x=(-200\pm200)/(-32) \\ x=(-200+200)/(-32)=(0)/(-32)=0\text{ and }x=(-200-200)/(-32)=(-400)/(-32)=12.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w2eqvr4vhezz54mc62f945e0hwkb4okv4a.png)
Then the two x-values are x=0 and x=12.5.
The starting time is 0 and the end time when the ball hit the ground is x=12.5.
The ball actually hung in the air 12.5 seconds.