Question

If 180° ≤ ≤ 270 and S(A) = −4 then determine the exact values of cos(A) and tan(A)

Answer 1

Recall the definition of the sine of an angle on a right triangle:

`\sin (A)=(a)/(c)`

On the other hand, according to this diagram, the values for tan(A) and cos(A) are given by:

`\begin{gathered} \cos (A)=(b)/(c) \\ \tan (A)=(a)/(b) \end{gathered}`

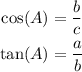
Since 180≤A≤270, the right triangle that corresponds to the angle A on the coordinate plane looks as follows:

Where a and b are negative distances.

Since sin(A)=-4/7, we can assume that a=-4 and c=7. Use the Pythagorean Theorem to find the exact value of b:

`\begin{gathered} a^2+b^2=c^2 \\ \Rightarrow(-4)^2+b^2=7^2 \\ \Rightarrow16+b^2=49 \\ \Rightarrow b^2=49-16 \\ \Rightarrow b^2=33 \\ \Rightarrow|b|=\sqrt[]{33} \end{gathered}`

We know that b should be negative. Then:

`b=-\sqrt[]{33}`

Substitute b=-sqrt(33) and c=7 to find the exact values for cos(A) and tan(A):

`\begin{gathered} \cos (A)=-\frac{\sqrt[]{33}}{7} \\ \tan (A)=\frac{-4}{-\sqrt[]{33}}=\frac{4\cdot\sqrt[]{33}}{33} \end{gathered}`

Therefore, the exact values for cos(A) and tan(A) are:

`\begin{gathered} \cos (A)=-\frac{\sqrt[]{33}}{7} \\ \tan (A)=\frac{4\cdot\sqrt[]{33}}{33} \end{gathered}`