As given by the question
There are given that the two-point;
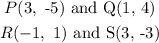
Now,
First, find the slope of both of the lines from the point
Then,
For first line:

Now,
For the second line:
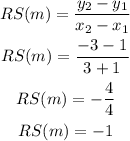
Since both slopes are different, they are not parallel lines, which means parallel lines have the same slope.
Hence, the correct optio