The formula used to calculate the perimeter of a rectangle is given to be:
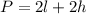
FIRST BOX
For the first orange box, we have that:
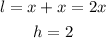
Note that the box is divided into 2 parts.
Therefore, this perimeter is:
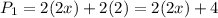
SECOND BOX
For the second orange box, we have that:
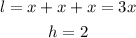
Note that the box is divided into 3 parts.
Therefore, the perimeter is:
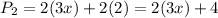
Using the associative property of multiplication, we have that:
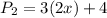
Since x = 5, we have:
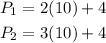
where 2 and 3 are the number of divisions of the boxes.
If we represent the number of divisions with x, we have the perimeter's function to be:
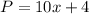
ANSWER
The correct option is the THIRD OPTION.