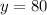We can find the y-intercept evaluating the function for x = 0, so:
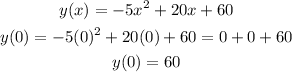
---------
We can find the zeros evaluating the function for y = 0. So using the factored form:
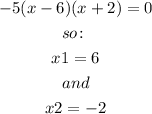
-----------------------------------------------
The vertex V(h,k) is given by:
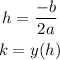
Or we can find it directly from the vertex form:
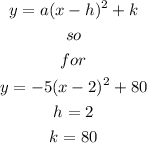
So, the vertex is:
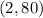
---------
The symmetry axis is located at the same point of the x-coordinate of the vertex, so the axis of symmetry is:
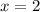
-----------------------
The maximum value is located at the y-coordinate of the vertex (if it is positive) so, the maximum value is: