a) b) c) d)
1) Examining each function, let's test considering that the average rate of change is given by:
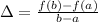
2) So let's plug the functions:
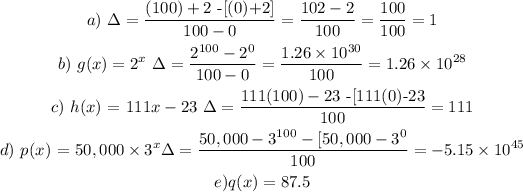
3) Since the average rate of change is a "measure of how much a function changes in the given interval" and considering that we have linear and exponential functions and the last one e) is not a function but an equation.
Then we can say that for the functions below the average rate of change is a good measure, not applying for the last one which, indeed is not a function.
a)
b)
c)
d)