Question

Twice a number, decreased by 4, is at least 12. Which of the following is a solution?8576

Answer 1

8

Explanation:

Let the number = n

Twice the number decreased by 4:

`2n-4`

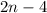
The phrase 'at least' means the expression above can either be equal to or greater than 12.

Thus, the given statement as inequality is:

`2n-4\geq12`

We then solve the inequality for n.

`\begin{gathered} \text{ Add 4 to both sides} \\ 2n-4+4\geq12+4 \\ 2n\geq16 \\ \text{ Divide both sides by 2} \\ (2n)/(2)\geq(16)/(2) \\ n\geq8 \\ \implies n=(8,9,10,\cdots) \end{gathered}`

The number that is a solution is 8.