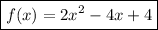Step 1. We are given the vertex of the quadratic function:
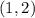
And a point:

Required: Find the standard form of the quadratic equation.
Step 2. Since we know the vertex of the quadratic function we will start by using the vertex form of the quadratic function:

Where (h, k) is the vertex, in this case:
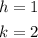
Step 3. To use the previous equation
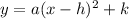
We will need to find the value of a. For that, we substitute the h and k values:
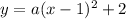
And as the values of x and y, we substitute the values of the given point (2,4) where x=2 and y=4
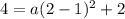
Solving for a:
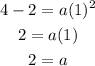
Step 4. Now that we know that the value of a is 2, we go back to our general equation:
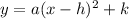
Substitute the value of a, h, and k:
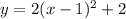
This is the equation in the vertex form, but we need it in standard form.
Step 5. The standard form of the quadratic function is:

To convert our equation into the standard form, first, we change y by f(x):

Then, we use this formula for the binomial squared:
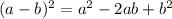
The result is:
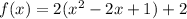
Simplifying:
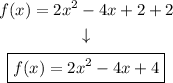
That is the standard form of the quadratic function.
Answer: