The first thing we have to know is that a cube with numbers is a dice that has 6 faces and that its numbers go from 1 to 6, so the probability that the sum of both dice gives 1 is zero, since the minimum that we are going to give is 2
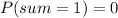
Now for the sum of both dice of 4 we have the following combinations
• 1 and 3
,
• 3 and 1
,
• 2 and 2
We have 3 combinatorics that we have to get the probability of each of the combinations in order to find our final probability
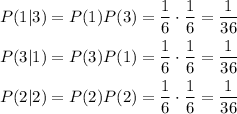
The probability that the sum of 4 would be the sum of the probabilities of the combinatorcs
What is the probability of getting a 1 and a 4 in either order?
The probability of getting any number on a die will be 1/6 if we can get a 1 or a 4 then our population will be 2/6
