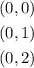Question

A) Find the points of intersection between the curve y = x(x - 1) (x - 2) and x-axis.

Answer 1

To find the intersection of the curve

`y=x(x-1)(x-2)`

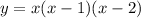
And the x-axis, we first have to notice that the x-axis is the same as the line:

`y=0`

Now, we have a system of two equations.

If we substitute y = 0 into the first, we have:

`x(x-1)(x-2)=0`

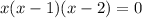
Now, for this equation to be true, one of the factors, "x", "(x-1)" or "(x-2)" has to be zero.

So, we will have three solutions:

`\begin{gathered} x=0 \\ x-1=0\leftrightarrow x=1 \\ x-2=0\leftrightarrow x=2 \end{gathered}`

And since these are on the x-axis, we already know that the y values for them are all y = 0.

Thus, the points of intersections are:

`\begin{gathered} (0,0) \\ (0,1) \\ (0,2) \end{gathered}`