Question

A farmer has 36 ft of fencing and wants to enclose the maximum rectangular area for his llamas. Find the dimensions of three possible areas he could enclose. What do you think the maximum area is? Why?

Answer 1

The farmer would like to eclose a rectangle

First we know that the perimeter of the rectangle is

`P=2x+2y`

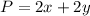
We also know that we have 36 ft of fence, that is we only can enclose a rectangle of 36 ft of perimeter. Then

`36=2x+2y`

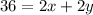
From this we can find y

`\begin{gathered} 36=2x+2y \\ 36-2x=2y \\ y=(36-2x)/(2) \\ y=18-x \end{gathered}`

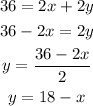
The area of the rectangle is

`A=xy`

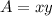
But we know the value of y, plugging this value into the last equation we have that

`A=x(18-x)`

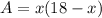
To find three possible values for the area we only have to give values to x. This values have to be positive (since we can't have a negative lenght). We also notice that the value can't exceed 18 since that would mean a zero area. With those point in consideration we choose three values between zero and 18.

If x=3, then the area is

`\begin{gathered} A=3(18-3) \\ =3(15) \\ =45 \end{gathered}`

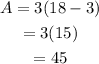
If x=9, then the area is

`\begin{gathered} A=9(18-9) \\ =9(9) \\ =81 \end{gathered}`

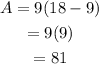
if x=15, then the area is

`\begin{gathered} A=15(18-15) \\ =15(3) \\ =45 \end{gathered}`

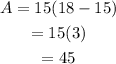
Then we have three possible areas for the rectangle.

The maximum value for the area is 81, and we see that because the equation for the area is a parabola that opens down with vertex in the point (9,81)