To check the decay rate, we need to check the variation in y-axis.
Since our interval is
![-2We need to evaluate both function at those limits.<p></p><p>At x = -2, we have a value of 4 for both of them, at x = 0 we have 1 for the exponential function and 0 to the quadratic function. Let's call the exponential f(x), and the quadratic g(x).</p><p></p>[tex]\begin{gathered} f(-2)=g(-2)=4 \\ f(0)=1 \\ g(0)=0 \end{gathered}]()
To compare the decay rates we need to check the variation on the y-axis of both functions.
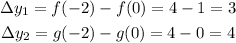
Now, we calculate their ratio to find how they compare:
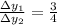
This tell us that the exponential function decays at three-fourths the rate of the quadratic function.
And this is the fourth option.