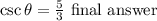Question

An angle has a cosine of 4/5. What will its cosecant be?

Answer 1

Recall that the cosine ratio is determined by adjacent side, divided by the hypotenuse of a right triangle.

Given that cosine is 4/5, the opposite side is

`\begin{gathered} a^2+b^2=c^2 \\ a^2+(4)^2=(5)^2 \\ a^2+16=25 \\ a^2=25-16 \\ a^2=9 \\ √(a^2)=√(9) \\ a=3 \end{gathered}`

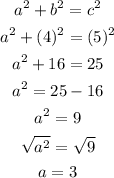
Now that we have solved for the opposite side, recall that cosecant is determined by the equation

`\csc\theta=\frac{\text{hypotenuse}}{\text{opposite}}`

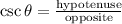
Substitute

hypotenuse = 5

opposite = 3

and we get

`\csc\theta=(5)/(3)\text{ \lparen final answer\rparen}`