Question

connie is packing for a trip. she has 16 pairs of shoes. if she has room to pack 7 pairs, how many ways can she choose which shoes to take?

Answer 1

Combinatorics

If Connie had only 7 pairs of shoes and she has room for 7 pairs of shoes, then she has only one way to take her shoes.

If she had 8 pairs of shoes, then she can select any group of shoes that leaves one pair out. This makes 8 possible ways to choose.

When the number of pairs of shoes goes up, then the counting gets more complex. That is when combinatorics is a useful tool.

If we have a total of n elements to select m, where the order of selection is not important, then the total number of selections is given by:

`C_(n,m)=(n!)/((n-m)!\cdot m!)`

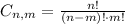
Where the sign (!) is the factorial of a number.

Connie has n=16 pairs of shoes and she will take m=7 from them, thus the number of possible ways or combinations is:

`\begin{gathered} C_(16,7)=(16!)/((16-7)!\cdot7!) \\ C_(16,7)=(16!)/((9)!\cdot7!) \end{gathered}`

Expanding the factorial down to match the greatest factorial in the denominator:

`C_(16,7)=(16\cdot15\cdot14\cdot13\cdot12\cdot11\cdot10\cdot9!)/((9)!\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)`

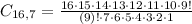
Simplifying and calculating:

`C_(16,7)=(57,657,600)/(5,040)=11,440`

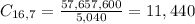
Connie can choose in 11,440 ways the shoes to choose