Question

In the diagram below of circle A. diameter MP = 26. m_GAI = 30° and radiGA and Al are drawn.MАP30°G1if MG IP, find the area of the sector MAG in terms of me and approximateto the nearest hundredth.The area of the sector in terms of u isTTThe area of the sector rounded to the nearest hundredth isunitssquared.

Answer 1

To find the area of a sector of a circle in terms of π having the angle in degrees you use the next formula:

`A=(\theta)/(360)\cdot\pi\cdot r^2`

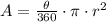
r is the radius

To find area of sector MAG:

1. Find the angle of the sector MAG.

The semicircle has an angle of 180° and it is divided into 3 sectors MAG, GAI, and IAP.

As the arcs MG and IP are congruents (have the same measure) the angles of the sectors MAG and IAP are also congruent.

`\begin{gathered} m\angle\text{MAG}+m\angle\text{GAI}+m\angle\text{IAP}=180 \\ \\ m\angle MAG=m\angle IAP \\ m\angle GAI=30 \\ \\ 2m\angle MAG+m\angle GAI=180 \\ 2m\angle MAG+30=180 \end{gathered}`

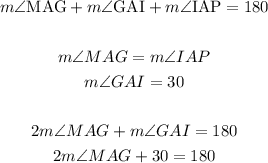
Use the equation above to find the measure of angle MAG:

`\begin{gathered} 2m\angle MAG=180-30_{} \\ 2m\angle MAG=150 \\ m\angle MAG=(150)/(2) \\ \\ m\angle MAG=75 \end{gathered}`

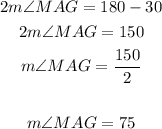
2. Find the area of sector MAG:

Angle 75°

radius= half of the diameter (26/2 = 13)

r=13

`\begin{gathered} A=(75)/(360)\cdot\pi\cdot(13)^2 \\ \\ A=(75)/(360)\cdot\pi\cdot169 \\ \\ A=(12675)/(360)\pi \\ \\ A=(845)/(24)\pi \\ \\ A\approx35.21\pi \\ \\ A\approx110.61 \end{gathered}`

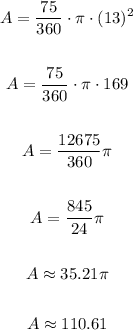
The exact area of the sector MAG is 845/24 π units squared.

Rounded to the nearest hundredth 35.21 π units squared or 110.61 units squared