Question

To find the height of a display in a museum, a person place a mirror on the ground 35ft from the display. Then he stepped back 5ft so he could see the top of the display. His eyes were about 5'4" from the ground. What is the height of the display?(ill send the image because it was to big)

Answer 1

Now let's calculate the angle of the first triangle. We will use the tangent function because we have information from the opposite side and the adjacent side.

`\begin{gathered} \tan \theta=\frac{5\text{ ft 4''}}{5\text{ ft}} \\ \end{gathered}`
`\begin{gathered} \theta=\tan ^(-1)(1.0666) \\ \theta=46.84\text{ degree} \end{gathered}`

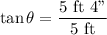
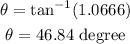
With this angle we can calculate the height of the display. Again we will use the tangent function.

`\begin{gathered} \tan (46.84)=(x)/(35) \\ x=35\cdot\tan (46.84) \end{gathered}`
`x=37.33\text{ ft}`

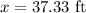
The answer would be 37.33 ft the height of the display