Question

50th term 64 57 50 43...

Answer 1

hello

to solve this question, we need to know if this sequence is an arithmetic or geometric progression

first term (a) = 64

common difference (d) = -7

the nth term of an arithemetic progression is given as

`\begin{gathered} T_n=a+(n-1)d_{} \\ n=\text{nth term} \\ a=\text{first term} \\ d=\text{common difference} \end{gathered}`

now let's substitute the values into the equation above

`\begin{gathered} T_n=a+(n-1)d_{} \\ a=64 \\ d=-7 \\ T_(50)=64+(50-1)*-7 \\ T_(50)=64+(49*-7) \\ T_(50)=64+(-343) \\ T_(50)=64-343 \\ T_(50)=-279 \end{gathered}`

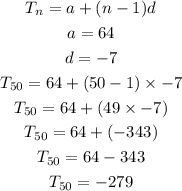
from the calculations above, the 50th term of the sequence is -279