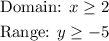Question

2) y = -5 +4V7-2 A) Domain: { All real numbers. } Range: { All real numbers. } B) Domain: x 22 Range: y 2-5 + C) Domain: 'x z 2 Range: ys-5 D) Domain: x 2-2 Range: y z 5

Answer 1

Looking at the restrictions over the variable x, we know that the domain is:

`x\ge2`

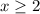
To find the range, notice that:

`\sqrt[]{x-2}\ge0`

On the other hand, the function:

`y=\sqrt[]{x-2}`

is an increasing function (its value grows when x grows), and can get as large as we want provided a sufficiently large value for x. Then, the range of such a function would be:

`y\ge0`

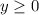
Which does not get altered when we multiply the square root of (x-2) by 4.

Since the function:

`y=-5+4\sqrt[]{x-2}`

is a 5-units shift downwards, then the variable y can take any value from -5 onwards.

Then, the range of the function is:

`y\ge-5`

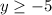
Another way to find the range is to isolate x from the equation:

`\begin{gathered} y=-5+4\sqrt[]{x-2} \\ \Rightarrow y+5=4\sqrt[]{x-2} \\ \Rightarrow(y+5)/(4)=\sqrt[]{x-2} \\ \Rightarrow((y+5)/(4))^2=x-2 \\ \Rightarrow x-2=((y+5)/(4))^2 \\ \Rightarrow x=((y+5)/(4))^2+2 \end{gathered}`

Since we already know that x must be greater than 2, then:

`\begin{gathered} 2\le x \\ \Rightarrow2\le((y+5)/(4))^2+2 \\ \Rightarrow0\le((y+5)/(4))^2 \\ \Rightarrow0\le|(y+5)/(4)| \\ \Rightarrow0\le|y+5| \end{gathered}`

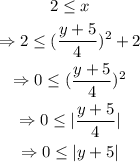
From here, there are two options:

`\begin{gathered} 0\le y+5 \\ \Rightarrow-5\le y \\ \text{ Or} \\ 0\le-y-5 \\ \Rightarrow y\le-5 \end{gathered}`

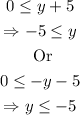
Since we know an equation for y, then:

`\begin{gathered} -5\le-5+4\sqrt[]{x-2} \\ \Rightarrow0\le4\sqrt[]{x-2} \end{gathered}`

Or:

`\begin{gathered} -5+4\sqrt[]{x-2}\le-5 \\ \Rightarrow4\sqrt[]{x-2}\le0 \end{gathered}`

The second case is not true for every x.

Therefore:

`-5\le y`

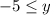
Therefore:

`\begin{gathered} \text{Domain: }x\ge2 \\ \text{Range: }y\ge-5 \end{gathered}`