Question

If a || b, m<2=63°, and m<9=105°, find the measure of missing angle m<1=?

Answer 1

Given:

a.) ∠9 = 105°

b.) ∠2 = 63°

Step 1: Determine the measure of ∠10.

∠9 and ∠10 are Supplementary Angles. This means that the sum of the two angles is equal to 180°.

From this, we generate the following equation:

`\text{ }\angle9\text{ + }\angle10=180^(\circ)`

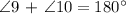
Let's then now proceed to find out the measure of ∠10.

`\text{ }\angle9\text{ + }\angle10=180^(\circ)`
`\text{ }105^(\circ)\text{ + }\angle10=180^(\circ)`
`\angle10=180^(\circ)\text{ - }105^(\circ)`
`\angle10=75^(\circ)`

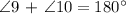
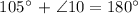
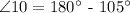
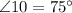
Step 2: Determine the measure of ∠3.

∠10 and ∠3 are Alternate Exterior Angles. Under this, the two angles must be congruent.

`\text{ }\angle3\text{ = }\angle10`

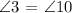
Therefore,

`\text{ }\angle3\text{ = }\angle10`
`\text{ }\angle3=75^(\circ)`

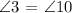
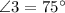
Step 3: Determine the measure of ∠1.

∠1, ∠2 and ∠3 are also Supplementary Angles. This means that the sum of the three angles is equal to 180°.

Thus, we generate the equation below:

`\text{ }\angle1\text{ + }\angle2\text{ + }\angle3=180^(\circ)`

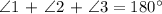
Let's now find the measure of ∠1,

`\text{ }\angle1\text{ + }\angle2\text{ + }\angle3=180^(\circ)`
`\text{ }\angle1\text{ + }63^(\circ)\text{ + }75^(\circ)=180^(\circ)`
`\text{ }\angle1\text{ + }138^(\circ)=180^(\circ)`
`\text{ }\angle1\text{ }=180^(\circ)\text{ - }138^(\circ)`
`\text{ }\angle1\text{ }=42^(\circ)`

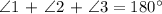
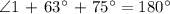
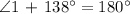
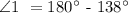
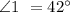
Therefore, the measure of ∠1 is 42°.