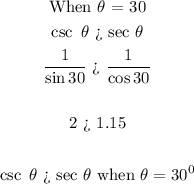SOLUTION:
(i)
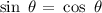
Sine of an angle is complementary to the Cosine of an angle so for both to be the same the angle 90 degrees must be divided into.
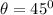
(ii)
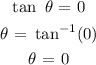
(iii)
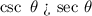
As said earlier sine and cosine of angles are complementary so cosecant and secant of angles are also complementary.