Given:
There are given that the Jotham needs 12 litters of 20% alcohol solution.
Step-by-step explanation:
Let x be the volume of the 50% solution needed
Then,
The volume of the 10% solution to mix is:
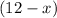
Then,
The equation to find x is:
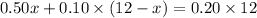
That means,
It say that the volume of the pure alcohol in ingredients is equal to the volume of pure alcohol.
Then,
From the above equation, calculate the value of x
So,
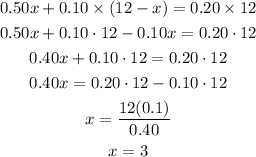
Final answer:
For the 50%, there are 3 litters solution and for the 10%,
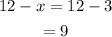
Hence, 3 liters of the 50% solution and 9 liters of the 10% solution.