Given:
The eyuation of the parabola.
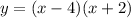
Required:
We need to find the x-intercepts, vertex, and standard form of the equation.
Step-by-step explanation:
Set y =0 and solve for x to find the x-intercepts of the parabola.
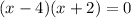
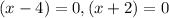
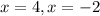
The x-intercepts are 4 and -2.
Multipy (x-4) and (x+2) to find the stansdad form of the equation.
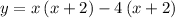
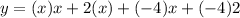
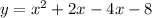
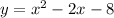
The standard form of the equation is
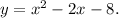
which is of the fom
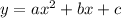
where a =1, b =-2 and c =-8.
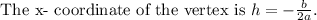
Substitute b =-2 and a =1 in the equation.
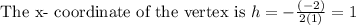
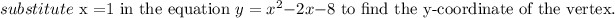
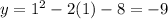
The vertex of the given parabola is (1,-9).
Final answer:
1)
The x-intercepts are 4 and -2.
2)
The standard form of the equation is
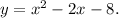
3)
The vertex of the given parabola is (1,-9).