Question

Which polynomial function is graphed below?-10A. (x) = (x – 3yº (x + 2)B. f(x) = (x - 2y(x +3)C. (*) - (x - 2)(x+3)D. *(x) = (x-3)(x + 2y4

Answer 1

Every polynomial can be written in the form:

`f(x)=(x-a_1)(x-a_2)\ldots_{}`

The a_1, a_2.... are the roots of the polynomial, meaning that f(a_1) = f(a_2) = ... = 0. This happens wen the graph of the polynomial intersects or tangency the x-axis. Whe it only tangecy the x-axis, it means that you have two of the root.

In this case, we have the polynomial tangency the x-axis in x = -2 and intersect the x-axis in x = 3. This means that the polynomial has roots -2, -2 (again) and 3. So:

`\begin{gathered} f(x)=(x-(-2))(x-(-2))(x-3) \\ f(x)=(x+2)(x+2)(x-2) \\ f(x)=(x+2)^2(x-3) \end{gathered}`

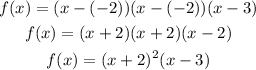
Since the order doesn't metter, we can right in this way:

`f(x)=(x-3)(x+2)^2`

Which corresponds to alternative D.