Question

Graph AABC with A(4, 7), B(0,0), and C(8, 1).a. Which sides of AABC are congruent? How do you know?b. Construct the bisector of ZB. Mark the intersection of the ray and AC as D.c. What do you notice about AD and CD?

Answer 1

a) Two sides of a triangle are concruent when they are the same length. First calculate the lenght of each side

`\begin{gathered} AC^2=\text{ (X\_c-X\_a)}^2+(Y_a-Y_c)^2=(8-4)^2+(7-1)^2=\text{ 52} \\ AC=√(52)=7.2 \end{gathered}`
`\begin{gathered} AB^2=(X_a-X_b)^2+(Y_a-Y_b)^2=(4-0)^2+(7-0)^2=\text{ 65} \\ AB=√(65)=8.06\approx8 \end{gathered}`
`\begin{gathered} BC^2=(X_c-X_b)^2+(Y_c-Y_b)^2=(8-0)^2+(1-0)^2=\text{ 65 } \\ BC=√(65)=8.06\approx8 \end{gathered}`

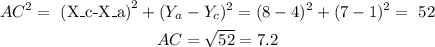
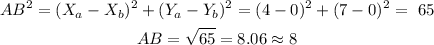
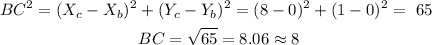
Sides AB and BC aren congruent.

b)

The bisector divides the triangle in exact halves.

The bisector is the blue line, in green you'll se the length of each side.

c)