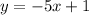The Slope-Intercept form of the equation of the line is:

Where "m" is the slope of the line and "b" is the y-intercept.
The slope can be found with:

Choose two points from the table. These could be the points (1,-4) and (4,-19). You can set up that:

Substituting values, you get that the slope of this line is:
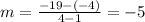
You can substitute the slope and the first point into the equation in Slope-Intercept form:
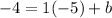
Solve for "b":
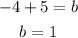
Therefore, the Equation of this line in Slope-Intercept form is: