Problem:
You and your sister have six-sided dice each one. What is the probability that if both roll your dice, you get an even number and your sister get an odd number.
Now, each dice has 6 numbers: 1,2,3,4,5,6
The even numbers are: 2,4,6 (3 options)
The odd numbers are: 1,3,5 (3 options)
Now, the probability of rolling an even number is:
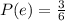
And the probability of rolling an odd number is:

Then, the probability that you get an even number and your sister an odd number is the product of the probabilities of each event:
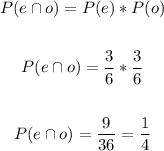
The probability is 1/4