To solve for x you can first divide by 12 into both sides of the equation, like this
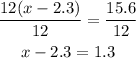
Now, you can add 2.3 from both sides of the equation

Therefore, the value of x that satisfies the equation is

Finally, to check that this value satisfies the given equation, just plug x = 3.6 into the equation and see that a true proposition is reached. So, you have
