Question

The Quadratic f(x)=x^2-2x-15Using the functions of your graphing calculator calculate the coordinates of the following points (as shown in the calculator videos in this lesson). If the parabola doesn't intersect the x-axis then write "none." If necessary, round to the nearest hundredths place (2 decimal places).a. The vertex using the min/max calculate function.b. X-intercept(s) using the zero calculate function.c. Y-intercept using the value calculate function (w/ a value of x=0).d. Now, copy down the t-table generated by your calculator for integer input values from-3≤x≤3.

Answer 1

Given: The function below

`f(x)=x^2-2x-15`

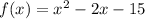
To Determine: The vertex, the x-intercept, the y-intercept, and the table for -3≤x≤3

Solution

The graph of the given function is as shown below

Hence:

The vertex is a minimum value at y = -16 and coordinate (1, -16)

(b) The X-intercepets is x = -3, x = 5, coordinates: (-3, 0) and (5, 0)

(c) The Y-intercept is at y = -15, coordinate: (0, - 15)

(d) The table showing the values of f(x) for -3≤x≤3 is as shown below