Question

-Quadratic Equations- Determine the number and the nature of the solutions to (3a + 24)² = -36 and then solve

Answer 1

There are two solutions and they are both complex solutions. The solutions are:

`a=2i-8;a=-2i-8`

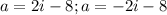
Step-by-step explanation

We want to determine the number and nature of solutions to the equation:

`(3a+24)^2=-36`

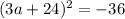
To do this, solve the equation by first, finding the square root of both sides of the equation:

`\begin{gathered} \sqrt[]{(3a+24)^2}=\pm\sqrt[]{-36}=\pm\sqrt[]{-1\cdot36} \\ \Rightarrow3a+24=\pm\mleft\lbrace\sqrt[]{36}\cdot\sqrt[]{-1}\mright\rbrace \\ 3a+24=\pm6i \end{gathered}`

Now, solve the equation for a:

`\begin{gathered} 3a=\pm6i-24 \\ \Rightarrow a=\pm(6i)/(3)-(24)/(3) \\ \Rightarrow a=2i-8;a=-2i-8 \end{gathered}`

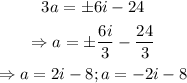
Hence, there are two solutions and they are complex solutions.