Given:
Velocity at t = 0: 80 m/s
Velocity at t = 10.0 s: 167 m/s
Let's find the distance it covered between t = 2.0s and t = 6.0 s
Apply the kinematics formula:
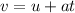
Where:
v is the final velocity ==> 167 m/s
u is the initial velocity ==> 80 m/s
a is the acceleration
t is the time ==> 10.0 - 0 = 10.0 s
Now, let's find the acceleration.
Rewrite the formula for a:
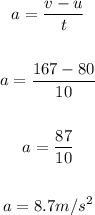
The acceleration is 8.7 m/s²
To find the distance, apply the formula:
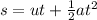
Thus, we have:
• At t = 2.0 s:
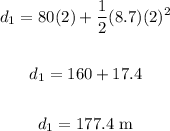
• At t = 6.0 s:
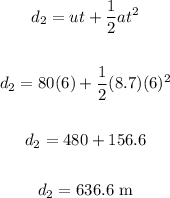
To find the distance traveled between t = 2.0 s and t = 6.0 s, we have:
d = d2 - d1 = 636.6 m - 177.4 m
d = 459.2 m
Therefore, the distance traveled betwen t = 2.0 s and t = 6.0 s is 459.2 m
ANSWER:
459.2 m