ANSWER
Step-by-step explanation
The ratio between corresponding sides of similar triangles is constant - in other words, the ratio between each pair of corresponding sides gives the same value.
As shown in the questions, the ratios between corresponding sides are,
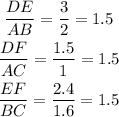
Since the three ratios between corresponding sides are the same, 1.5, the triangles are similar.