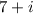Answer:
The remaining zero is;
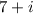
Step-by-step explanation:
Given that two of the zeros of a polynomial are;
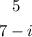
to get the remaining zero.
Recall that according to complex conjugates, complex roots/zeros comes in pairs;
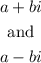
where a and b are real numbers.
Applying the rule to the given roots.
Since we have a complex root;
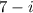
we must also have the other pair of the complex root;
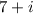
Therefore, the remaining zero is;