Question

Suppose that the dollar value v () of a certain house that is t years old is given by the following exponential function.v (t) = 637,000 (1.02)^tFind the initial value of the house.s1Does the function represent growth or decay?O growth O decayBy what percent does the value of the house change each year?

Answer 1

ANSWER:

• (a). 637000 dollars

,

• (b). Growth

,

• (c). 2%

Answer 2

Given the function:

`v(t)=637000(1.02)^t`

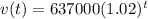
Where:

v(t) represents the value of the house after t years.

Let's find the following:

• (a). Find the initial value of the house.

Apply the exponential function:

`f(x)=a(b)^x`

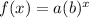
Where:

a is the initial value

b is the growth of decay factor.

Here, we have:

a = 637000

b = 1.02

Therefore, the initial value of the house is 637,000 dollars.

• (b). Does the function represent growth or decay?

If b is greater than 1 the function represents a growth function.

If b is less than 1, the function represents a decay function.

Here, we have:

b = 1.02

Therefore, the function represents a growth function.

• (c). By what percent does the value of the house change each year?

Apply the formula:

`f(x)=a(1+r)^x`

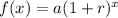
Where r is the growth rate.

Thus, to find r, we have:

1 + r = 1.02

r = 1.02 - 1

r = 0.02

The growth rate is 0.02

To convert the rate to percent multiply by 100:

Growth percent = 0.02 x 100 = 2%

Therefore, the value of the house increases by 2% each year.

ANSWER:

• (a). 637000 dollars

,

• (b). Growth

,

• (c). 2%