We have to calculate the perimeter of a pen that has an area expressed as
A = 3x²-7x+2.
We assume it is a rectangular pen, so it will have two different sides.
The area will be the product of this two side lengths, while the perimeter will be 2 times the sum of the lengths of the two sides.
Then, we start by rearranging the expression of A as a product of two factors.
We can do it by factorizing A.
To do that, we calculate the roots of A as:
![\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4\cdot3\cdot2}}{2\cdot3} \\ x=\frac{7\pm\sqrt[]{49-24}}{6} \\ x=\frac{7\pm\sqrt[]{25}}{6} \\ x=(7\pm5)/(6) \\ \Rightarrow x_1=(7-5)/(6)=(2)/(6)=(1)/(3) \\ \Rightarrow x_2=(7+5)/(6)=(12)/(6)=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/z211epkcwl865kgi2ihmw7ou8whpt89xb8.png)
Then, we can now express A as:
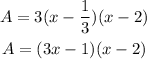
Then, we can consider the pen to be a rectangle (or maybe square, depending on the value of x) with sides "3x-1" and "x-2".
Then, we can now calculate the perimeter as 2 times the sum of this sides:
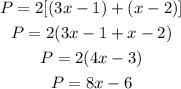
Answer: we can express the perimeter as 8x-6.