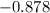The function we have is:
![f(x)=\frac{\sqrt[]{x}-7}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/yxp032wt38ss3a3dy5tky9ybbwo5ox5p7p.png)
And we need to find the value of f(3).
To solve this problem and find f(x), we need to substitute x=3 into the given function.
• Substituting x=3 into f(x) to find f(3):
![f(3)=\frac{\sqrt[]{3}-7}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/yjrwm7rtdevyl18eylyp1pp9uruxgl50iu.png)
And now, we start solving the operations.
Since the square root of 3 is equal to 1.732:
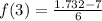
Substracting 7:
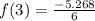
And finally, dividing by 6:
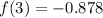
To round to the nearest thousandth we need to round to 3 decimal places, which in this case we already have, thus, the final answer is: