Question

Please help solve the following questions using the exponential equation

Answer 1

We want to solve

`7^(2x+4)=2^(x-5)`

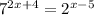
Taking logarithm of both sides, we have

`\begin{gathered} \log 7^(2x+4)=\log 2^(x-5) \\ (2x+4)\log 7=(x-5)\log 2 \\ \text{expanding we have } \\ (2x)\log 7+(4)\log 7=(x)\log 2-(5)\log 2 \end{gathered}`

Collecting like terms we have

`\begin{gathered} (2x)\log 7-(x)\log 2=-(4)\log 7-(5)\log 2 \\ x(2\log 7-\log 2)=-4\log 7-5\log 2 \\ \text{dividing both sides by }(2\log 7-\log 2),\text{ we have } \\ x=(-4\log 7-5\log 2)/(2\log 7-\log 2) \end{gathered}`

Hence the solution set expressed in terms of logarithm is

`x=(-4\log7-5\log2)/(2\log7-\log2)`

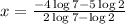
Using a calculator to obtain a decimal approximation, we have

`\begin{gathered} x=(-4\log7-5\log2)/(2\log7-\log2) \\ x=(-3.3804-1.5051)/(1.6902-0.3010) \\ x=(-4.8855)/(1.3892) \\ x=-3.51677 \\ x=-3.52 \end{gathered}`

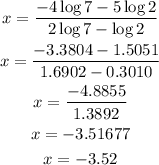
Hence the answer is -3.52 to 2 decimal places