Question

Consider the following function.f(x) = |x − 9|Find the derivative from the left at x = 9. If it does not exist, enter NONE.Find the derivative from the right at x = 9. If it does not exist, enter NONE.

Answer 1

The form of the derivative of the absolute equation is

`\begin{gathered} f(x)=\lvert x-a\rvert \\ (dx)/(dy)=(\lvert x-a\rvert)/(x-a) \\ (dy)/(dx)=(x-a)/(\lvert x-a\rvert) \end{gathered}`

For the given function

`f(x)=\lvert x-9\rvert`

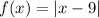
We will find the derivative from the left at x = 9

`(dy)/(dx)=(x-9)/(\lvert x-9\rvert)`

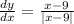
Substitute x by 9

`\begin{gathered} (dy)/(dx)=(9-9)/(\lvert9-9\rvert) \\ (dy)/(dx)=(0)/(0) \end{gathered}`

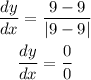
Then dy/dx does not exist (None)

The derivative from right at x = 9

`(dx)/(dy)=(\lvert x-9\rvert)/(x-9)`

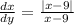
Substitute x by 9

`\begin{gathered} (dx)/(dy)=(\lvert9-9\rvert)/(9-9) \\ (dx)/(dy)=(0)/(0) \end{gathered}`

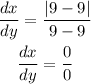
Then dx/dy does not exist (None)