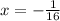Question

Given the exponential equation:, find a common base and solve for x.

Answer 1

Step-by-step explanation:

Given;

We are given the exponential equation shown below;

`((125)/(8))^(4x-1)=((4^2)/(25^2))^(x+1)`

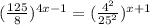
Required;

We are required to

(i) Find a common base

(ii) Solve for x

Step by step solution;

To solve this problem we shall start with the following steps;

`[((5)/(2))^3]^(4x-1)=[((2)/(5))^4]^(x+1)`

For the left side of the equation, we can refine by applying the rule of exponents;

`\begin{gathered} Flip\text{ the left side of the equation:} \\ ((2)/(5))^(-3) \end{gathered}`

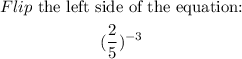
Therefore, we now have;

`[((2)/(5))^(-3)]^(4x-1)=[((2)/(5))^4]^(x+1)`
`((2)/(5))^(-12x+3)=((2)/(5))^(4x+4)`

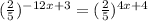
We now have a common base and that means;

`\begin{gathered} If: \\ a^x=a^y \\ Then: \\ x=y \end{gathered}`

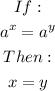
Therefore;

`-12x+3=4x+4`
`-12x-4x=4-3`
`-16x=1`

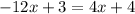
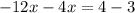
Divide both sides by -16;

`x=-(1)/(16)`

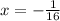
ANSWER:

`x=-(1)/(16)`