Question

Reduce to lowest term.4x-24/x^2-36

Answer 1

`(4)/((x-6))`

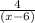
Step-by-step explanation

`(4x+24)/(x^2-36)`

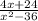
Step 1

factorize

`\begin{gathered} a)\text{ 4x+24} \\ if\text{ we rewrite 24 as a product of its factors} \\ 4x+24=4x+(6\cdot4) \\ 4x+(6\cdot4)\rightarrow4\text{ is a common factor, so }\rightarrow4(x+6) \end{gathered}`

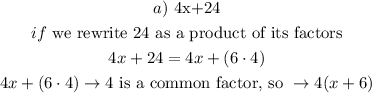
and the denominator

we have

`b)x^2-36`

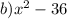
remember:When an expression can be viewed as the difference of two perfect squares, it can be factorized this way

`\begin{gathered} a^2-b^2=(a+b)(a-b) \\ \end{gathered}`

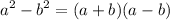
so, apply this .

`\begin{gathered} x^{^{}2}-36=x^2-6^2=(x+6)(x-6) \\ so,\text{ } \\ x^{^{}2}-36=(x+6)(x-6) \end{gathered}`

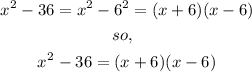
hence, the expression would be:

`(4x+24)/(x^2-36)=(4(x+6))/((x+6)(x-6))`

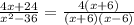
Step 2

finally, eliminate the (x+6) ,so

`\begin{gathered} (4(x+6))/((x+6)(x-6))=(4)/((x-6)) \\ (4)/((x-6)) \end{gathered}`

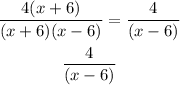
therefore, the lowest term is

`(4)/((x-6))`

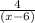
I hope this helps you